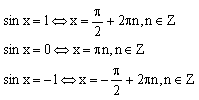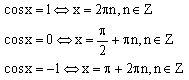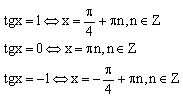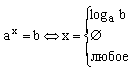Методы решения уравнений
Линейные уравнения (ax+b=0)
1) если а=0 и b=0 Þ
x-любое 2) если а=0 и b¹0 Þ Æ
3) если а¹0 и b¹0 Þ x=
Квадратные
уравнения (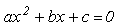 ,
a¹0)
,
a¹0)
 ,
где
,
где 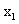 и
и
 -
корни соответствующего уравнения
-
корни соответствующего уравнения
1) если D<0 – Æ 2) если D=0
 3)
если D>0
3)
если D>0 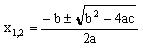 ,если
b-четно, то
,если
b-четно, то 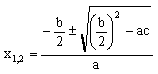
 -
теорема Виета
-
теорема Виета
Если
кубическое уравнение общего вида разделить на а, то коэффициент при 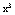 станет
равен 1. Поэтому уравнение примет вид
станет
равен 1. Поэтому уравнение примет вид 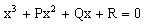 .
По формуле куба суммы имеем
.
По формуле куба суммы имеем 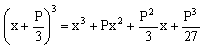 .
Сложим оба уравнения и приведем подобные:
.
Сложим оба уравнения и приведем подобные: 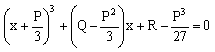 .
Если сделать замену
.
Если сделать замену  ,
получим кубическое уравнение вида
,
получим кубическое уравнение вида 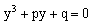 .
Итак, мы показали, что в кубическое уравнение общего вида можно привести к
уравнению
.
Итак, мы показали, что в кубическое уравнение общего вида можно привести к
уравнению 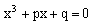 .
Поэтому формулу корней дадим для него:
.
Поэтому формулу корней дадим для него:
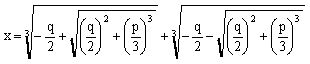 -
формула Кардано
-
формула Кардано
Для нахождения других корней
уравнения стоит решить уравнение  ,
где h - корень, найденный по формуле Кардано.
,
где h - корень, найденный по формуле Кардано.
Тригонометрические уравнения (сводятся к уравнениям вида
sinx=a,
cosx=a, tgx=a,
ctgx=a)


Имеют место так называемые общие случаи:
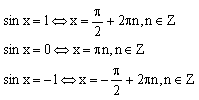
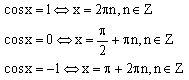
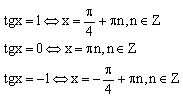

Показательные уравнения ( )
)
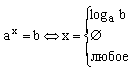

Логарифмические уравнения ( ,
,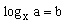 )
)
Необходимо
учитывать, что подлогарифмическое выражение больше нуля, а основание
логарифма больше нуля и отлично от единицы.



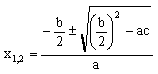
 -
теорема Виета
-
теорема Виета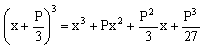 .
Сложим оба уравнения и приведем подобные:
.
Сложим оба уравнения и приведем подобные: 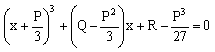 .
Если сделать замену
.
Если сделать замену 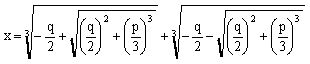 -
формула Кардано
-
формула Кардано